Lecture: "Quantum Computing 1 & 2" by Prof. J. Wrachtrup, Dr. Florian Kaiser
Quantum Computers and Applications
The goal of the course is to provide a comprehensive overview of the current state-of-the-art quantum computation. The course comprises a lecture (2h/week) plus a tutorial (2h every second week). Students will have the opportunity to do semester projects in which they e.g. work with real quantum computers, learn their programming and use for problem solving.
The module can be selected as elective module in B.Sc., M.Sc. and M.Ed. Physics (9 ETCS) and as area of specialization module in M.Sc. Physics (12 ECTS points) with an additional Quantum Computing internship.
| Lecturers: | Prof. J. Wrachtrup, Dr. Florian Kaiser |
| Beginning: | Wednesday, November 4th, 2020 |
| Lecture Time: | Wednesday, 9:45 - 11:15 |
| Location: | Lecture will be held as live conference (first 2 weeks), also videos and additional material of the lecture will be provided on ILIAS. |
| More Information: | Presentation of the module on ILIAS |
| Language: | English |
| Examination: | Oral (in German or English) |
| Scope: | 2 SWS lecture, 1 SWS exercise |
| Number: |
043151000 |
| Selectable as: |
|
Module 1: Quantum Computing 1
The physics of information
Landauer’s principle, Reversible Computing, Maxwells demon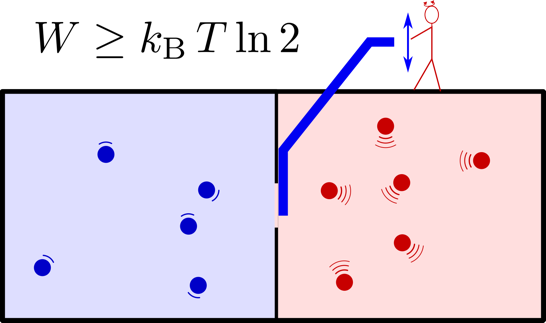
Quantum bits
DiVincenco Criteria, Initialization, Gates, Example: P in Si,
Elements of Classical Computer Science
Boolean Algebra and logic gates, Universal computers, Complexity classes,
Quantum Mechanics for Quantum Computation
Quantum mechanics of quantum gates, Relaxation and Dephasing, Density matrix
Quantum gates and first simple algorithm
NOT-, CNOT-Gate, Density matrix tomography, CNOT for spin and ion trap qubits, Deutsch-Jozsa algorithm,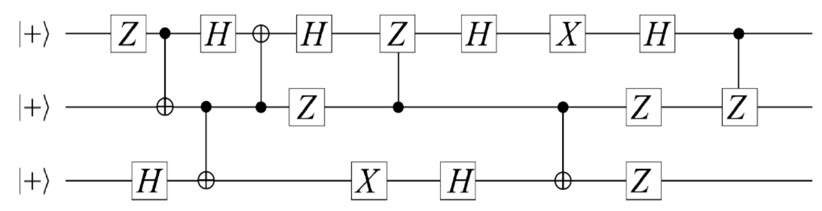
Quantum Error Correction
Error bounds, Majority vote, Stabilizer Formalism, Fault tolerant quantum computing,
Experimental Quantum Error Correction
Majority vote spins, Superconducting Qubits: 5Qubit error detecting code
How to build a Quantum Computer
Superconducting QC, Ion Trap Quantum Computer
Figure 1: Image source: IBM
Module 2: Quantum Computing 2
Shor algorithm
Public Key Cryptography, Period finding, Quantum Fourier Transformation, Implementation of Shor algorithm
Figure 2: Image source: iStock
Quantum Fourier Transformation
Efficient Implementation of QFT, Example: 4 Qubit QFT, Experiments: nuclear magnetic resonance and ion trap quantum computing.
Phase estimation and Grover search algorithm
Precision limits in phase estimation, QFT for phase estimation, Defining oracles for Grover search, example: 3 qubit search.
Quantum random walks
Classical vs. quantum walk, quantum coin, calculate permanent of matrix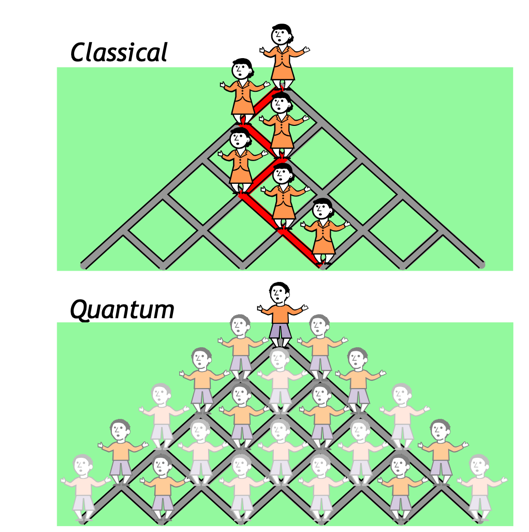
Figure 3: Image source: AIP
Quantum Chemistry
Molecular electronic Hamiltonian in 2nd quantisation, Jordan-Wigner transformation, Trotter decomposition, Components of circuit, Phase estimation for molecular energies, Example: Hydrogen molecule.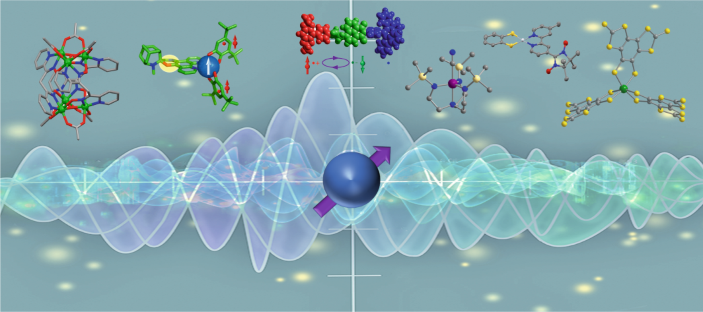
Figure 4: Image source: Nature
Quantum classical hybrid algorithm
Variational quantum eigensolver, MaxCut problem,
Introduction to quantum machine learning
k-nearest neighbors, HHL Algorithm, Eigenvalue inversion, Quantum principle component analysis
Quantum communication and Repeaters
Quantum key distribution, Single photon sources, Eckart protocol and CHSH inequality, Quantum memory, lambda-systems, EIT, DLCZ protocol.
Figure 5: Image source: QTech Delft
The previous lectures of the institute take place in German and will be shown on the following page.


