Science and teaching at the institute comprises solid state quantum optics and spintronics with applications in modern microscopy and metrology applications in e.g. biophysics. Common to all experimental approaches is the use of photons as central tool. Besides set-ups in the field of optics and spin control facilities at the institute comprise synthesis, implantation and structuring of carbon materials, protein purification and cell culturing.
New Highlight
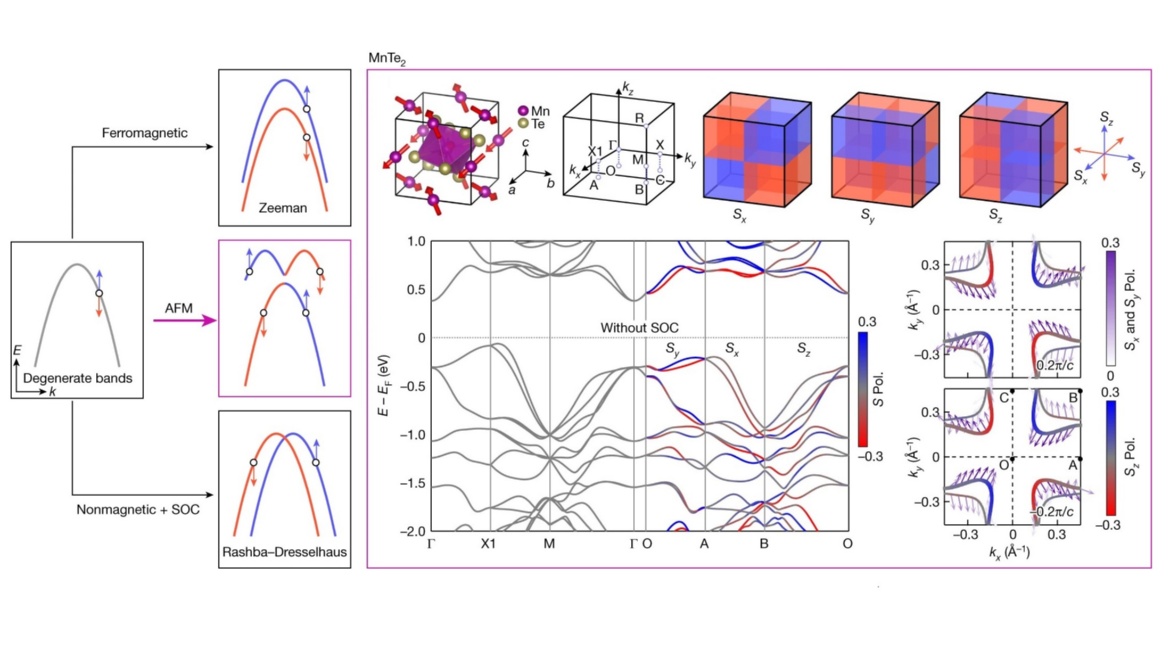
Observation of plaid-like spin splitting in a noncoplanar antiferromagnet
News
Diamond Materials for Quantum Application
23. September 2014: The DFG research group FOR 1493 “Diamond Materials and Quantum Applications” goes into its second funding period. FOR1493 is a national research consortium funded by the Deutsche Forsch-ungsgemeinschaft.
European Research Council
Established by the European Commission
Supporting top researchers from anywhere in the world.
Contact

Jörg Wrachtrup
Prof. Dr.Head of Department
[Photo: David Ausserhofer]

Sabrina Jenne
MScOffice